인공 신경망

패션 MNIST

딥러닝에서 MNIST가 유명함 -> 손으로 쓴 0~9까지 숫자 자료. 패션 MNIST는 숫자 대신 패션 아이템으로 이루어짐

from tensorflow import keras

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()

60,000개의 28*28 이미지로 되어 있음

print(train_input.shape, train_target.shape)
print(test_input.shape, test_target.shape)

(60000, 28, 28) (60000,)

(10000, 28, 28) (10000,)

import matplotlib.pyplot as plt

fig, axs = plt.subplots(1, 10, figsize=(10,10))
for i in range(10):
    axs[i].imshow(train_input[i], cmap='gray_r')
    axs[i].axis('off')
plt.show()

print([train_target[i] for i in range(10)])

[9, 0, 0, 3, 0, 2, 7, 2, 5, 5]

패션 아이템의 종류를 나타내고 있다. 종류는 아래와 같다

import numpy as np

print(np.unique(train_target, return_counts=True))

(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000]))

label별로 item이 몇개씩 있는지 확인했고, 각 60000개씩 있는 것을 볼 수 있다.

로지스틱 회귀로 패션 아이템 분류하기

훈련 샘플이 6만개라 전체를 한꺼번에 하기보다는 하나씩 꺼내서 모델을 훈련하는 것이 좋다.

이럴 때 사용하는 것이 확률적 경사 하강법(SGDClassifier)

train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28*28)
print(train_scaled.shape)

(60000, 784)

from sklearn.model_selection import cross_validate
from sklearn.linear_model import SGDClassifier

sc = SGDClassifier(loss='log', max_iter=5, random_state=42)

scores = cross_validate(sc, train_scaled, train_target, n_jobs=-1)
print(np.mean(scores['test_score']))

0.8195666666666668

max_iter=5는 SGDClassifier 반복 횟수

인공신경망

텐서플로와 케라스

import tensorflow as tf
from tensorflow import keras

인공신경망으로 모델 만들기

from sklearn.model_selection import train_test_split

train_scaled, val_scaled, train_target, val_target = train_test_split(
    train_scaled, train_target, test_size=0.2, random_state=42)

print(train_scaled.shape, train_target.shape)
print(val_scaled.shape, val_target.shape)

(48000, 784) (48000,)

(12000, 784) (12000,)

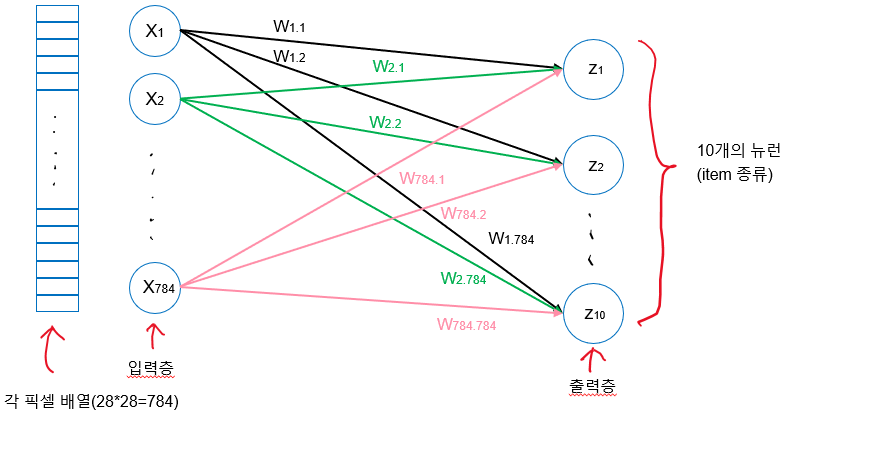
dense = keras.layers.Dense(10, activation='softmax', input_shape=(784,))
model = keras.Sequential(dense)

인공신경망으로 패션 아이템 분류하기

model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
print(train_target[:10])

[7 3 5 8 6 9 3 3 9 9]

model.fit(train_scaled, train_target, epochs=5)

Epoch 1/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.6097 - accuracy: 0.7913
Epoch 2/5
1500/1500 [==============================] - 2s 2ms/step - loss: 0.4785 - accuracy: 0.8396
Epoch 3/5
1500/1500 [==============================] - 2s 2ms/step - loss: 0.4557 - accuracy: 0.8479
Epoch 4/5
1500/1500 [==============================] - 2s 2ms/step - loss: 0.4438 - accuracy: 0.8519
Epoch 5/5
1500/1500 [==============================] - 2s 2ms/step - loss: 0.4362 - accuracy: 0.8547

<keras.callbacks.History at 0x7f253d669550>

결과가 할 때마다 다르게 나온다. 그러나 충분히 안정적으로 된다면 차이가 크지 않다.

model.evaluate(val_scaled, val_target)

375/375 [==============================] - 1s 1ms/step - loss: 0.4475 - accuracy: 0.8494

[0.44751664996147156, 0.8494166731834412]

* 인공 신경망

 - 뉴런에서 영감을 받아 만든 머신 러닝 알고리즘. 딥러닝으로 불리기도 함

* 텐서플로

 - google library. CPU/GPU를 사용해 훈련. 케라스 사용

* 밀집층

 - 가장 간단한 신경망의 층. 뉴런들이 모두 연결되어 있기 때문에 완전 연결층이라고도 부름

 - 특별히 출력층에 밀집층을 사용할 때는 분류하려는 클래스와 동일한 개수의 뉴런을 사용

* 원-핫 인코딩

 - 정숫값을 배열에서 해당 정수 위치의 원소만 1이고 나머지는 모두 0으로 변환

 - 필요한 이유 => 다중 분류에서 출력층에서 만든 확률과 크로스 엔트로피 손실을 계산하기 위함

 - 텐서플로에서 'sparse_categorical_entropy' 손실을 지정하면 이런 변환이 필요 없음

TensorFlow

 * Dense

 - 밀집층을 만드는 class

 - activation : 활성화 함수 지정(sigmoid, softmax), 지정하지 않을 수도 있음

 * Sequential 

 - 케라스에서 신경망 모델을 만드는 클래스

 - 추가할 층이 1개 이상일 경우 파이썬 리스트로 전달

 * compile()

 - 모델 객체를 만든 후 훈련하기 전에 사용할 손실 함수와 측정 지표 등을 지정

 - loss : 손실함수 지정(binary_crossentropy : 이진 분류, categorical_crossentropy : 다중 분류, sparse_categorical_crossentropy : 클레스 레이블이 정수, mean_square_error : 회귀 모델)

 * fit() : 훈련

 * evaluate() : 평가

* 결정트리 Decision Tree

 - 스무고개와 같이 질문을 하나씩 던져 정답을 맞춰가며 학습하는 알고리즘 -> 예측 과정을 이해하기 쉬움

* 검증세트 Validation set

 - hiperparameter 튜닝을 위해 모델을 평가할 때, test set을 사용하지 않기 위해 훈련 세트에서 다시 떼어낸 data set

* 교차검증 cross validation

 - 훈련세트를 여러 폴드로 나눈 다음 한 폴드가 검증 세트의 역할을 하고 나머지 폴드에서는 모델을 훈련

* 그리드 서치 Grid Search

 - hiperparameter 탐색을 자동화 해주는 도구 -> 자동으로 맞는 값을 찾아준다

* 랜덤 서치 Random Search

 - 연속적인 parameter의 값을 탐색할 때 유용

* 정형데이터(structured data) vs 비정형데이터(unstructured data)

 - CSV, database등 특정 구조로 되어 있는 것은 structed data, 정형화가 어려운 사진, 음악 등은 비정형 데이터라고 함

* 앙상블 학습 ensemble learning

 - 여러 알고리즘을 합쳐 성능을 높이는 머신러닝 기법

* 랜덤 포레스트 Random Forest

 - 대표적인 앙상블 학습 방법, 안정적인 성능

 - 부트스트랩 샘플 사용, 랜덤하게 일부 특성을 선택하여 트리를 만든다

* 부트스트랩 샘플 Bootstrap sample

 - 데이터세트에서 중복을 허용하여 데이터를 샘플링하는 방식

* 엑스트라 트리 extra trees

 - random forest와 비슷하게 동작하며 결정 트리를 사용하여 앙상블 모델을 만들지만 bootstrap sample을 사용하지 않는 대신 랜덤하게 노드를 분할하여 과대적합을 감소

* 그레이디언트 부스팅 Gradient boosting

 - 깊이가 얕은 결정 트리를 사용하여 이전 트리의 오차를 보완하는 방식으로 앙상블하는 방법, 깊이가 얕은 결정 트리를 사용하기 때문에 과대적합에 강하고 일반적으로 높은 일반화 성능을 기대할 수 있음

* Histogram-based Gradient Boosting

 - Gradient boosting의 속도를 개선한 것으로 과대적합을 잘 억제하며 Gradient boosting

차원 축소:

원본 데이터의 특성을 적은 수의 새로운 특성으로 변환하는 비지도 학습. 저장 공간을 줄이고 시각화 하기 좋음, 다른 알고리즘의 성능 향상

주성분 분석(Principal Component Analysis : PCA):

데이터에서 가장 분산이 큰 방향을 찾는 방법.( 이 방향을 주성분이라 한다) 일반적으로 주성분은 원본 데이터에 있는 특성 개수보다 작다.

설명된 분산:

주성분 분석에서 주성분이 얼마나 원본 데이터의 분산을 잘 나타내는지 기록한 것. 사이킷런의 PCA class는 주성분 개수나 설명된 분산의 비율을 지정하여 주성분 분석을 수행할 수 있다.

* 이미지를 예로 들면 모든 픽셀이 특성이 되는데 이를 모두 기록하기는 어렵다. 이들 특성 중 주성분을 분석하여 분산에 맞게 저장하는 방법을 학습한다. 또한 이렇게 저장된 내용으로 다시 원본 데이터에 가깝게 복구가 가능하다.

* 분산이 크다는 것은 data가 가장 멀리 퍼진 방향을 나타낸다. 점들이 직선에 가깝게 퍼져 있다면 이러한 직선이 data의 특성을 잘 나타낸다고 볼 수 있다.

PCA Class

!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np

fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)

from sklearn.decomposition import PCA

pca = PCA(n_components=50)
pca.fit(fruits_2d)

PCA(n_components=50)

PCA가 찾은 주성분이 componenctes_에 들어가 있다.

print(pca.components_.shape)

(50, 10000)

배열의 차원이 50이다.(주성분 50)

import matplotlib.pyplot as plt

def draw_fruits(arr, ratio=1):
    n = len(arr)    # n은 샘플 개수입니다
    # 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다. 
    rows = int(np.ceil(n/10))
    # 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
    cols = n if rows < 2 else 10
    fig, axs = plt.subplots(rows, cols, 
                            figsize=(cols*ratio, rows*ratio), squeeze=False)
    for i in range(rows):
        for j in range(cols):
            if i*10 + j < n:    # n 개까지만 그립니다.
                axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
            axs[i, j].axis('off')
    plt.show()
draw_fruits(pca.components_.reshape(-1, 100, 100))

주성분을 50으로 잡았으니 특성의 개수를 10,000에서 50으로 줄일 수 있다.

transform()을 이용하여 원본 데이터의 차원을 50으로 줄일 수 있다.

print(fruits_2d.shape)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)

(300, 10000)

(300, 50)

원본 데이터 재구성

fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)

for start in [0, 100, 200]:
    draw_fruits(fruits_reconstruct[start:start+100])
    print("\n")

줄어든 특성을 이용하여 다시 원본 데이터를 복구하였는데 거의 비슷한 결과를 볼 수 있다.

미분 후 적분한 것처럼 손실은 있다.

설명된 분산

print(np.sum(pca.explained_variance_ratio_))
plt.plot(pca.explained_variance_ratio_)
plt.show()

0.9214965686302707

50개의 주성분이 있으나 처음 10개의 주성분이 대부분의 분산을 표현하고 있다.

다른 알고리즘과 함께 사용하기

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression()

target = np.array([0] * 100 + [1] * 100 + [2] * 100)

from sklearn.model_selection import cross_validate

scores = cross_validate(lr, fruits_2d, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))

0.9966666666666667 : test score

1.5750249862670898 : fit time

scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))

1.0 : 50개의 주성분으로 분석했을 때 정확도가 100%로 나왔다

0.025466299057006835 : fit time 역시 엄청 줄었다.

pca = PCA(n_components=0.5)
pca.fit(fruits_2d)

PCA(n_components=0.5)

처음에는 주성분의 개수를 50개로 지정했는데 분산의 50%가 채워질 때까지 주성분의 개수를 늘리도록 변경하였다.

이렇게 변경한 다음 주성분의 개수가 몇개나 필요한 지 확인해보자.

print(pca.n_components_)

2

두개의 주성분이면 충분하다고 한다.

fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)

(300, 2)

scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))

0.9933333333333334 : test score

0.036731719970703125 : fit time

특성을 두개만 사용해도 99.3%의 정확도를 나타낸다.

from sklearn.cluster import KMeans

km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_pca)

KMeans(n_clusters=3, random_state=42)

print(np.unique(km.labels_, return_counts=True))

(array([0, 1, 2], dtype=int32), array([110, 99, 91]))

for label in range(0, 3):
    draw_fruits(fruits[km.labels_ == label])
    print("\n")

for label in range(0, 3):
    data = fruits_pca[km.labels_ == label]
    plt.scatter(data[:,0], data[:,1])
plt.legend(['apple', 'banana', 'pineapple'])
plt.show()

두개만 가지고 분류했는데 분산이 잘 이루어져 있다.

파인애플과 사과는 경계가 거의 붙어있어 혼동이 있을 수 있다.

(그런데 바나나는 왜 섞여 들어간거지?)