선택정렬(Selection Sort)
1. 선택정렬(Selection Sort)이란?
-. 실제 프로그래밍에서 많이 사용되는 간단한 정렬방법으로 오름차순을 기준으로 한다면,
최소값을 찾아 왼쪽으로 이동시키는데 배열크기만큼 반복하여 정렬하는 방법이다.
-. 가장 작은 값을 찾아서 첫번째 위치에 있는 값과 교환하고, 두번째로 작은 값을 찾아 두번째
위치에 있는 값과 교환하는 방법으로 이러한 방법을 반복한다.
2. 선택정렬을 이용하여 오름차순으로 정렬하는 방법
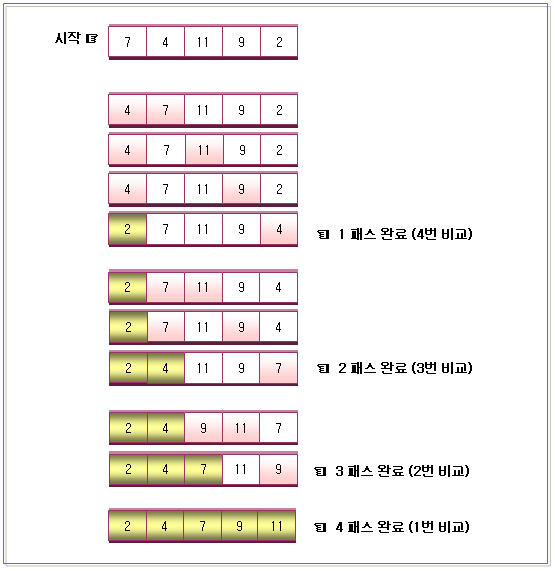
3. 선택정렬의 비교회수
-. 최선일 경우의 비교회수 공식 : N - 1
-. 최악일 경우의 비교회수 공식 : N(N – 1)/2
-. 위의 그림을 보시면 아시겠지만 제일 처음에는 (N – 1)번을 비교하고,
그 다음에는 (N – 2)번 만큼 비교하고, 그 다음은 (N – 3)번을 비교하면서 비교회수가 1이 될
때까지 이 작업을 반복할 것이다.
-. 비교회수는 (N – 1) + (N – 2) + (N – 3) …… + 1 이 될 것이다.
최대 (N – 1)번을 수행할 것이며, 각 패스가 수행할 때마다
수학식으로 표현하면 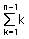
-. 5개의 값을 오름차순으로 선택정렬을 하면...
공식에 의해서 5(5 – 1)/2 = 10 가 성립된다.
즉, 총 10번의 비교를 통해서 오름차순으로 정렬된 값을 볼 수 있다.
4. 선택정렬의 연산시간
-. 연산시간 공식 : O(n²)
-. 연산시간을 표기하는 방법은 일반적으로 사용하는 O표기법인데, 이 O표기법은 ‘최악의 경우’
(Worst Case)에 대한 연산시간을 나타낸다.
-. 수학식으로 표현하면 아래와 같다.
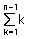 = n(n – 1) – (n – 1)/2 = n(n - 1)/2 이므로 Worst Case는 n(n – 1)/2 이다.
= n(n – 1) – (n – 1)/2 = n(n - 1)/2 이므로 Worst Case는 n(n – 1)/2 이다.
그래서 연산시간은 O(n²)가 되는 것이다.
5. 선택정렬의 장점
-. 데이터의 양이 적을 때 아주 좋은 성능을 나타낸다.
-. 작은 값을 선택하기 위해서 비교는 여러 번 하지만 교환횟수가 작다
6. 선택정렬의 단점
-. 가장 작은 값과 현재값을 교환하는 방식이라 현재값이 뒤쪽의 어디로 갈지 알 수 없으므로
안전성이 없다.
-. 100개 이상의 자료에 대해서는 속도가 급격히 떨어져서 적절히 사용되기가 힘들다.
7. 선택정렬을 이용해서 작성한 예제
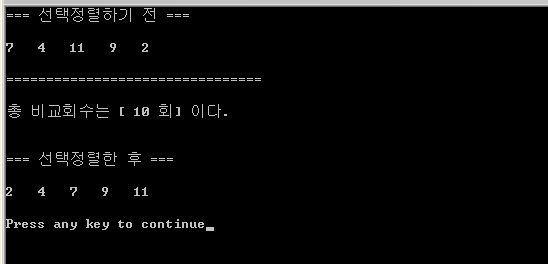
#include "stdio.h" void Select_Sort(int parm_data[], int parm_count) { int min_data = 0, min_index = 0; int i, j; int comparison_count = 0; for(i = 0; i < parm_count - 1; i++){ min_index = i; min_data = parm_data[i]; for(j = i + 1; j < parm_count; j++){ comparison_count++; if(min_data > parm_data[j]){ min_data = parm_data[j]; min_index = j; } } parm_data[min_index] = parm_data[i]; parm_data[i] = min_data; } printf("총 비교회수는 [ %d 회] 이다.", comparison_count); printf("\n\n\n"); } void main() { int array[5] = {7, 4, 11, 9, 2}; int i; printf("=== 선택정렬하기 전 ===\n\n"); for(i = 0; i < 5; i++) printf("%d ", array[i]); printf("\n\n"); printf("================================"); printf("\n\n"); Select_Sort(array, 5); printf("=== 선택정렬한 후 ===\n\n"); for(i = 0; i < 5; i++) printf("%d ", array[i]); printf("\n\n"); }
버블정렬(bubble sort)
1. 버블정렬이란? -. 인접해 있는 두 개의 값을 비교해서 자료 교환을 한다. -. 오름차순 정렬은 두 개의 값을 비교해서 큰 값을 오른쪽으로 보내는 방식이다, 내림차순 정렬은 두 개의 값을 비교해서 작은 값을 오른쪽으로 보내는 방식이다. 2. 버블정렬(Bubble Sort)과 유사한 용어
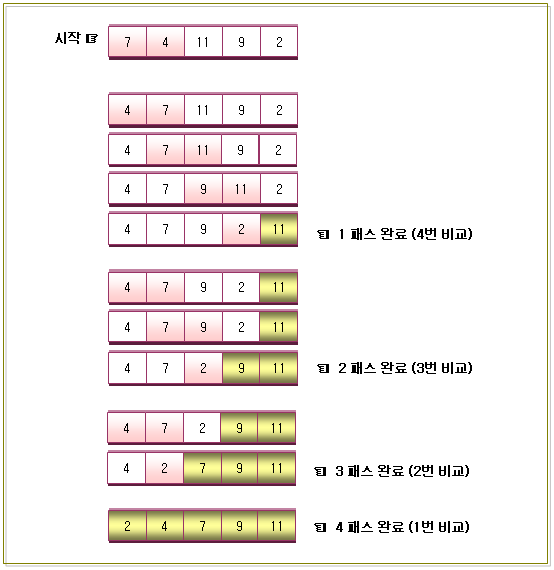
-. Interchange Sort -. Shifting Sort 3. 버블정렬을 이용하여 오름차순으로 정렬하는 방법 4. 버블정렬의 비교회수
-. 비교 회수 공식 : N(N – 1)/2 -. 위의 그림을 보시면 아시겠지만 제일 처음에는 (N – 1)번을 비교하고, 그 다음에는 (N – 2)번 만큼 비교하고, 그 다음은 (N – 3)번을 비교하면서 비교회수가 1이 될 때까지 이 작업을 반복할 것이다. -. 비교회수는 (N – 1) + (N – 2) + (N – 3) …… + 1 이 될 것이다. 최대 (N – 1)번을 수행할 것이며, 각 패스가 수행할 때마다 수학식으로 표현하면 -. 5개의 값을 오름차순으로 버블정렬을 하면...
공식에 의해서 5(5 – 1)/2 = 10 가 성립된다. 즉, 총 10번의 비교를 통해서 오름차순으로 정렬된 값을 볼 수 있다.
5. 버블정렬의 연산시간
-. 연산시간 공식 : O(n²) -. 연산시간을 표기하는 방법은 일반적으로 사용하는 O표기법인데, 이 O표기법은 ‘최악의 경우’ (Worst Case)에 대한 연산시간을 나타낸다. 6. 버블정렬의 장점 -. 인접해 있는 두 개의 값을 비교하여 자료의 위치를 이동시키므로 단순하다. -. 여러 차례 값을 비교하므로 안전성 있게 값을 정렬한다. 7. 버블정렬의 단점 -. 첫번째 패스에서 자료의 교환이 없었다면 주어진 값은 이미 오름차순으로 정렬된 상태이지만, 최대 N(N – 1)/2 만큼의 비교회수와 O(n²) 만큼의 연산시간이 소요된다. -. 다른 정렬에 비해서 연산시간이 오래 걸린다.
8. 버블정렬을 이용해서 작성한 예제
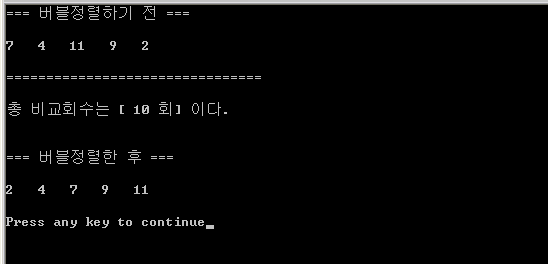
#include "stdio.h" void Bubble_Sort(int parm_data[], int parm_count) { int i, j, temp = 0; int comparison_count = 0; for(i = 0; i < parm_count - 1; i++){ for(j = 0; j < parm_count - 1 - i; j++){ comparison_count++; if(parm_data[j] > parm_data[j+1]){ temp = parm_data[j]; parm_data[j] = parm_data[j+1]; parm_data[j+1] = temp; } } } printf("총 비교회수는 [ %d 회] 이다.", comparison_count); printf("\n\n\n"); } void main() { int array[5] = {7, 4, 11, 9, 2}; int i; printf("=== 버블정렬하기 전 ===\n\n"); for(i = 0; i < 5; i++) printf("%d ", array[i]);
printf("\n\n"); printf("================================"); printf("\n\n"); Bubble_Sort(array, 5); printf("=== 버블정렬한 후 ===\n\n"); for(i = 0; i < 5; i++) printf("%d ", array[i]);
printf("\n\n"); }
버블 소트의 단점중에 이미 소트가 완료된 경우를 체크하지 못하고 계속 정렬을 시도하는 것입니다.
즉, 오름차순 정렬인데 데이터가 1,2,3,4 로 되어 있는 경우, 정렬할 필요가 없다는것을 알지
못하고 6번을 비교하게 됩니다. 따라서 이 부분을 고려할수 있도록 소스를 수정해서 사용하는
경우도 많습니다. 방법은 아래와 같습니다.
void Ex_Bubble_Sort(int parm_data[], int parm_count)
{
int i, j, temp = 0, flag = 1;
int comparison_count = 0;
for(i = 0; i < parm_count - 1; i++){
// 각 패스의 시작시점에서 flag값을 1로 설정한다.
flag = 1;
for(j = 0; j < parm_count - 1 - i; j++){
comparison_count++;
if(parm_data[j] > parm_data[j+1]){
// 자리 바꿈이 일어났다면 flag 값을 0으로 변경한다.
flag = 0;
temp = parm_data[j];
parm_data[j] = parm_data[j+1];
parm_data[j+1] = temp;
}
}
// flag값이 1이라는 소리는 한번도 자리바꿈이 일어나지 않았다는 뜻이다.
// 따라서 더 이상 정렬할 필요가 없다는 것으로 간주하여 종료한다.
if(flag == 1) break;
}
printf("총 비교회수는 [ %d 회] 이다.", comparison_count);
printf("\n\n\n");
}
퀵정렬(Quick Sort)
1. 퀵정렬(Quick Sort)이란?
-. 교환정렬의 일종이며 분할-정복법(divide and conquer)에 근거한다.
-. 정렬할 리스트를 두개로 분할하고 정렬하는 방법이다.
-. 축(pivot)값을 기준으로 정렬하는데, 축값을 중심으로 축값보다 큰 값은 오른쪽 리스트에
작은 값은 왼쪽리스트로 이동시킨다. (첫번째의 데이터를 축값으로 한다.)
-. 오른쪽 리스트와 왼쪽 리스트부분은 독립적인 단위로 정렬하여 오른쪽 리스트부분에 대한
새로운 분할 축값을 선택하여 두 부분으로 분리하고, 왼쪽 리스트부분 역시 새로운 축값을
선택하여 두 부분으로 분리하는 과정을 반복하는데 리스트들은 재귀적 방법으로 각각 재배열
하는 방식이다.
-. 각 분할 자료개수가 1이 되면 정렬은 완료된다.
2. 퀵정렬을 이용하여 오름차순으로 정렬하는 방법
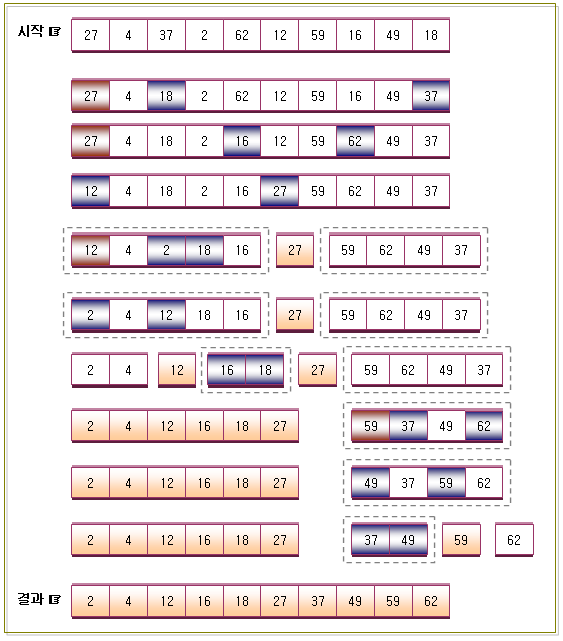
3. 퀵정렬의 비교회수
-. 최선일 경우의 비교회수 공식 : N - 1
-. 최악일 경우의 비교회수 공식 : N(N – 1)/2
-. 위의 그림을 보시면 아시겠지만 제일 처음에는 (N – 1)번을 비교하고,
그 다음에는 (N – 2)번 만큼 비교하고, 그 다음은 (N – 3)번을 비교하면서 비교회수가 1이 될
때까지 이 작업을 반복할 것이다.
-. 비교회수는 (N – 1) + (N – 2) + (N – 3) …… + 1 이 될 것이다.
최대 (N – 1)번을 수행할 것이며, 각 패스가 수행할 때마다
수학식으로 표현하면 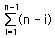
4. 퀵정렬의 연산시간
-. 연산시간 공식(평균) : 0(n log n)
-. 연산시간 공식(최악이 경우) : O(n²)
-. 연산시간을 표기하는 방법은 일반적으로 사용하는 O표기법인데, 이 O표기법은 ‘최악의 경우’
(Worst Case)에 대한 연산시간을 나타낸다.
5. 퀵정렬의 장점
-. 정렬할 데이터가 이미 준비되어 있고 모든 데이터들을 정렬해야 할 경우에 가장 빠른
수행속도를 보여준다.
6. 퀵정렬의 단점
-. 축(pivot)값이 같은 것끼리는 순서관계가 파괴된다.
(중요한 데이터의 경우에는 퀵정렬을 사용하지 않는 것이 좋다.)
-. 안정성이 없다.
7. 퀵정렬을 이용해서 작성한 예제
#include "stdio.h"
void Quick_Recursive(int parm_data[], int parm_left, int parm_right); void Quick_Sort(int parm_data[], int parm_count) { Quick_Recursive(parm_data, 0, parm_count - 1); } void Quick_Recursive(int parm_data[], int parm_left, int parm_right) { int pivot, left_hold, right_hold; left_hold = parm_left; right_hold = parm_right; // 0번째 원소를 pivot으로 선택한다. pivot = parm_data[parm_left]; while(parm_left < parm_right){ while((parm_data[parm_right] >= pivot) && (parm_left < parm_right)) parm_right--; if(parm_left != parm_right){ parm_data[parm_left] = parm_data[parm_right]; } while((parm_data[parm_left] <= pivot) && (parm_left < parm_right)) parm_left++; if(parm_left != parm_right){ parm_data[parm_right] = parm_data[parm_left]; parm_right--; } } parm_data[parm_left] = pivot; pivot = parm_left; parm_left = left_hold; parm_right = right_hold; if(parm_left < pivot) Quick_Recursive(parm_data, parm_left, pivot - 1); if(parm_right > pivot) Quick_Recursive(parm_data, pivot + 1, parm_right); } void main() { int array[10] = {27, 4, 37, 2, 62, 12, 59, 16, 49, 18}; int i; printf("=== 퀵정렬하기 전 ===\n\n"); for(i = 0; i < 10; i++) printf("%d ", array[i]); printf("\n\n"); printf("================================"); printf("\n\n"); Quick_Sort(array, 10); printf("=== 퀵정렬한 후 ===\n\n"); for(i = 0; i < 10; i++) printf("%d ", array[i]); printf("\n\n"); }
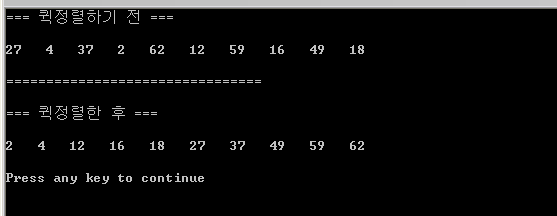
자료출처 : http://www.tipssoft.com
'Programming > C언어우려먹기' 카테고리의 다른 글
| 64bit 에서 int, long 사용 (0) | 2016.01.15 |
|---|---|
| 예외처리 scanf에서 이상한 값이 입력되었을 때. (4) | 2008.05.29 |
| 유클리드 호제법을 이용한 최대공약수, 최소공배수 계산 (0) | 2008.05.29 |
| factorial (재귀호출, 반복문) (0) | 2008.05.01 |
| 정렬 - 삽입정렬(Insert Sort), 힙정렬(Heap Sort), 쉘정렬(Shell Sort) (0) | 2008.04.27 |
| source C 완전제곱수 판별 (2) | 2008.03.19 |
| C언어에서 사용되는 연산자들(사실 C,C++,JAVA등 다양한 언어에서 공통적으로 사용된다.) (0) | 2008.03.10 |
| 무지간단한 주사위 통계 (0) | 2008.03.03 |
| 2진수로 표현하기 (0) | 2008.02.28 |